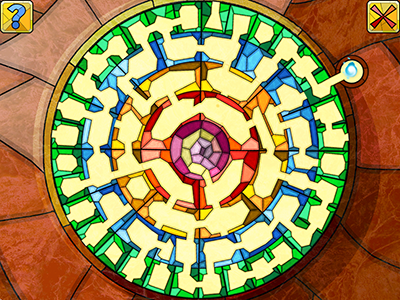
If you have already played Little Briar Rose, you probably have met the Mushroom Maze mini-game. You might have found out a solution alone, or maybe using the hint.
Some of you, instead, may have found new paths that we haven’t considered when developing the puzzle. That’s what we call a “miscalculation”.
While creating the puzzle, we knew that we could have put additional (unwanted) paths by mistake. However, we were certain that we could identify all of them during the testing phase.
We were wrong.
Just a day after the release, a few users reported a couple of paths that were not valid in the game, even if they were correct.
The mini-game is indeed simple. There’s a round labyrinth, made up of concentric circles of different sizes. Every circle can be rotated in order to create new paths. They contain many rooms neighboring, linked with different roads.
You have to create a valid path that could lead the spirit to the center of the maze.
How did we develop the puzzle?
The first idea was to create levels procedurally. We dropped it very soon, since it’s pretty hard to calibrate a procedural dungeon’s difficulty.
Instead, we moved to an old-fashioned but surely funnier approach:
We took scissors, paper, and markers, and we built a real-life version of the puzzles.
Starting from the actual solution, we introduced more dead-ends, shuffling the circle rotations.
Creating the first one was pretty simple, making sure that no fake-solution was introduced.
However, the more the puzzles were making complex, the more it was difficult to get rid of unwanted paths.
How have we fixed this?
We wanted to fix the issue as fast as possible. How to achieve this?
The simpler way was to explore all possible combination of states allowed in the labyrinth.
Let’s make some calculation. In the most complex puzzle, each circle can assume the following states:
- First circle: 8 positions
- Second: 16
- Third: 32
- Fourth and last: 64
In total: 8*16*32*64 = 262.144 combinations. Not bad
A player could (easily) solve this puzzle by excluding all roads that are visually dead ends. A computer just can’t.
How could a machine check for valid paths easily?
I considered to implement pathfinding algorithms, but it would have been really a long job: Even if the algorithm is well-known, I needed to map all rooms and roads to a graph that could be explored by an A* (or similar algorithms).
Finally, I tried a “visual” approach, using the most simple tool that every photo-editing application offers: The paint bucket. The algorithm used by this tool is the Flood Fill algorithm.
Starting from an input pixel of an image and a target color, it explores all adjacent pixels having a similar color of the input one. This is made recursively until all the similar-colored area is filled.
Here’s a sample gif from Wikipedia:

Here’s how I used the Flood Fill to identify valid paths in the maze:
- Set-up the mini game in a certain state, moving the circles accordingly
- Apply the flood fill, picking a pixel located near the spirit (the starting point)
- Check if the destination has been filled with the chosen color
- Repeat with another state
Here’s the Flood Fill Implementation in C#:
implementation notes:
I tried a recursive approach as well, that is a lot easier to implement.
However, it’s extremely slow and the application usually failed with a “Stack Overflow”.
Another interesting clue was to pre-allocate the stack size to a surely greater size than needed. Dynamic allocations are slow, moreover, it’s useful to identify bugs that could make the algorithm loop.
This allowed me to reduce execution times from seconds to milliseconds. Since I needed to apply this algorithm to more than 200k images, it’s pretty important.
Here’s a couple of outputs:
Here’s a gif of the running algorithm. Look how it rolls~
Thanks to this approach, we could identify more than 18 unwanted paths in the most complex puzzle. We could fix the bug in just a few hours, including the implementation.
Sometimes the simpler approach is the best!
Comments are welcome!